近年來,視覺測量因其高速、非接觸等特點廣泛應用于視覺定位、間距測量、尺寸測量等智能測量領域,其中包括齒輪的三維輪廓測量。目前,齒輪三維輪廓測量通常采用雙目視覺技術實現齒輪的三維點云數據提取及模型重構,但該方法獲取的齒輪初始點云往往離群點噪聲大、冗余性高,容易造成齒輪的三維重構質量差、尺寸測量精度低等問題,繼而影響齒輪的質量檢測及其制造精度。因此,亟需研究基于視覺測量的三維點云數據提取及其重構測量方法,以提高齒輪的三維重構測量精度。
國內外學者對三維重構技術開展一系列研究并取得諸多成果。Hoppe H 等人提出了一種面向無序點云的曲面重構算法,實現了曲面目標模型的平滑擬合。Gopi M 等人研究了二維空間Voronoi圖及Delaunay三角化,但該算法有較高的采樣密度要求。Morel J 等人提出了一種基于先驗模型的曲面重構算法,但該算法不適用于復雜的曲面模型重構。Wang W Y 等人采用 NURBS 進行了點云數據參數化與曲面重建,但其參數化后的重建效果受點云數據的散亂性影響。唐昀超等人提出一種基于雙目視覺的齒輪曲面重構算法,但該算法更適用于封閉的三維模型點云重構。
針對上述研究現狀及其存在的問題,本文首先利用雙目視覺測量系統獲取直齒圓柱齒輪的三維輪廓信息,分析并采用直通濾波和體素柵格濾波去除初始點云中的離群點及冗余點,通過除噪點減少數據處理量。然后采用移動最小二乘法平滑加貪婪三角化重構算法解決重構后表面粗糙、精度較低的問題。最后搭建雙目視覺齒輪測量系統實驗平臺,利用提取的齒輪三維點云數據進行三維模型重構,并分析齒輪重構效果及尺寸測量精度。
一、齒輪三維點云數據的獲取與分析
齒輪三維點云數據的測量原理
雙目立體視覺測量系統的結構原理如圖 1(a)所示,為了獲取齒輪的三維輪廓點云信息,利用左、右相機分別采集目標的圖像,根據左、右圖像的視差計算點的三維坐標。雙目視覺測量系統實驗平臺如圖 1(b)所示,其設備主要包括 2 組黑白工業相機、焦距 f 為 16 mm 的工業鏡頭、可調數字光學掃描頭、三腳架、齒輪、旋轉臺及計算機等。
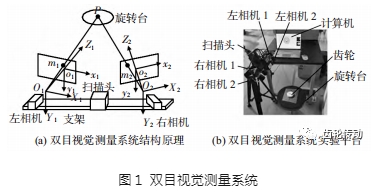
在圖 1 中,兩相機和掃描頭水平放置,O1 -X1Y1Z1 與 O2 -X2Y2Z2 分別為左、右相機坐標系,o1 -x1 y1 與 o2 -x2 y2 分別為左、右圖像坐標系,原點 O1 和 O2 分別為兩相機的光心,O1Z1 和 O2Z2 為兩相機的光軸。假設齒輪表面任意一 點 P 分別與 O1 、O2 連線,點 P 在平面 o1 x1 y1 和 o2 x2 y2 上的投影點坐標分別為 m1(x1 ,y1 )和 m2(x2 ,y2 ),將左相機的坐標系視為世界坐標系,則右相機可近似為一個單目相機模型,通過相機標定可獲得相機的旋轉矩陣 R 與平移矩陣 T。結合投影變換公式,可得到點 P 在世界坐標系下的三維坐標(X1 ,Y1 ,Z1 )如式(1)所示
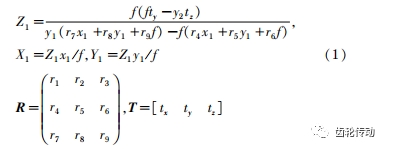
式中 f 為相機焦距。
齒輪三維點云特點分析
利用雙目視覺測量系統獲得的齒輪初始點云數據如圖 2 所示,點云數為 2 974 257,且圖中存在諸多離群點及冗余點。

根據上述齒輪初始點云數據,利用 Geomagic Control 軟件直接重構的齒輪三維模型如圖 3 所示,由圖可知重構后的齒輪表面凹凸不平,并且存在許多孔洞。

通過上述齒輪初始三維點云數據重構結果分析可知,采用雙目視覺系統進行尺寸三維模型重構時,需去除齒輪初始三維點云數據的離群噪點,并在保留表面信息的情況下去除冗余點云,保證重構后的表面更為平滑、孔洞更少,以提高齒輪尺寸的重構測量精度。
二、齒輪三維點云數據處理
點云去噪
為了提高齒輪的三維點云重構表面質量,本文采用直通濾波和體素濾波去除齒輪初始點云存在的離群點和冗余點等噪點。其中,直通濾波通過指定方向和值域來刪除不在值域范圍內的點,從而去除離群噪點。體素柵格濾波則在獲取點云坐標后,求得 X,Y,Z 坐標軸上的最大值xmax, ymax,zmax和最小值 xmin ,ymin ,zmin。給定邊長 v,則 X,Y,Z 坐標軸可以等分為 L,M,N 份,L =(xmax -xmin )/ v,M =(ymax - ymin )/ v,N =(zmax -zmin )/ v。
計算每個體素柵格的重心點,記為 cg,如式(2)所示, 每個體素柵格內只保留該重心點
式中 n 為體素柵格內數據點個數,pi 為數據點。經以上步驟,點云數據完成體素柵格濾波,去除了齒輪點云數據的大量冗余點云數據。
點云平滑
為了進一步提高齒輪三維模型重構精度及重構效果,本文采用移動最小二乘法進行點云數據平滑處理。建立擬合函數 f(x)如式(3)所示

權函數如式(4)所示,利用不同的基函數與權函數改變擬合曲面的光滑度與精度,從而完成點云數據平滑優化
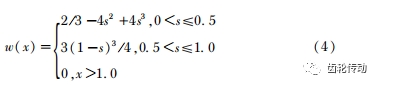
其中,s =ri / βhi,ri =‖x -xi‖,hi 為節點 xi 的權函數影響域的大小,β 為影響系數。
點云重構
基于上述去躁與平滑處理后的齒輪三維點云數據,本文采用貪婪三角化方法進行齒輪三維重建。貪婪三角投影算法具體流程如下:
首先,構建 kd-tree 索引,獲取種子點及 k 個鄰域點的信息。其次,給定一點 M0(x0,y0,z0 ),任取平面上一 點M(x,y,z),可得 M0 M·n =0,該切平面方程如式(5) 所示
利用式(6)所示的投影矩陣 T∏ ,將區域中的三維數據點投射到二維切平面上,進行三角網格化

式中 Tc 為平移變換矩陣,Rx 為圍繞 x 旋轉 α 角度,Ry 為圍繞 y 旋轉 θ 角度。
最后,遍歷完全部的數據點,最終形成齒輪的完整網格曲面。
三、實驗驗證
實驗方案設計
為了獲取齒輪的三維點云數據,驗證本文基于雙目視覺的齒輪三維點云重構方法的正確性與有效性。首先,搭建雙目視覺測量系統實驗平臺,如圖 1 所示,將齒輪置于旋轉臺中心,獲取當前視角下的齒輪數據后,將齒輪旋轉 45°直至旋轉一周得到完整的齒輪三維點云信息;其次,根據獲得的初始齒輪三維點云數據,采用直通濾波和體素濾波去除離群點和冗余點,完成點云降噪;然后,對比基于多項式平滑處理與移動最小二乘法 2 種方法下的齒輪尺寸測量精度,選用精度較高的方法進行點云平滑;最后,對比直接貪婪三角化重構、平滑貪婪三角化重構后獲得的齒輪模型,分別選取易于測量分析的齒頂圓直徑 D1、孔徑加鍵槽尺寸 D2、齒輪孔徑 D3 等尺寸進行測量精度分析,確定最佳的重構方法。
實驗結果與分析
直接重構的齒輪測量誤差分析:
為了分析直接重構的齒輪測量誤差,對未經任何圖像處理的齒輪初始三維點云數據直接進行重構和剖面截取,得到如圖 4 所示的齒輪剖面圖,并測量圖中 D1、D2、D3 參數尺寸,結果如表 1 所示。
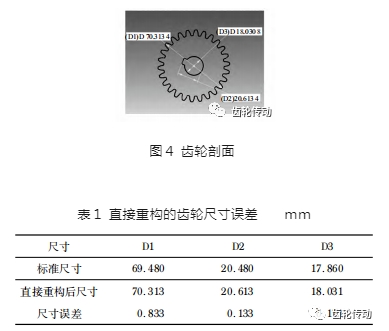
利用 50 分度值精密卡尺獲得待測齒輪的 D1、D2、D3 標準尺寸,與直接重構尺寸進行對比,可知 D1 尺寸的測量誤差為 0.833 mm,D2 測量誤差為 0.133 mm,D3 測量誤差為 0.171 mm。
濾波和平滑處理后的齒輪測量誤差分析:
為了提高齒輪三維點云重構效果及其尺寸測量精度,利用 2.1 節中的直通濾波去除初始點云中的離群點,同時在保留特征的情況下采用體素柵格濾波去除冗余點。濾波后的齒輪三維點云結果如圖 5 所示,初始點云數為 2 974 257,濾波后點云數為 215 999,由此可見,濾波處理可以在保留齒輪表面特征的同時精簡齒輪的點云數據。

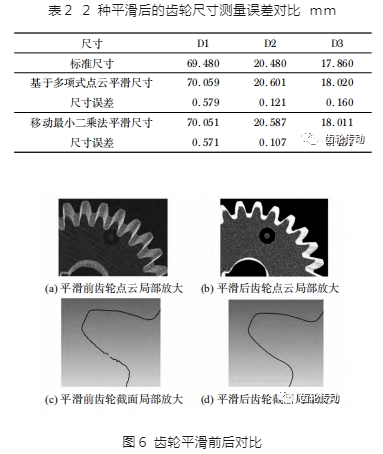
為了降低齒輪重構模型表面粗糙度并提高重構尺寸精度,分別采用基于多項式的平滑處理、移動最小二乘法平滑處理進行齒輪三維模型重構,獲得的齒輪 3 個尺寸數據及測量誤差如表 2 所示,經分析可知移動最小二乘法平滑后的齒輪尺寸誤差較小。采用移動最小二乘法平滑后的圖片如圖 6 所示,經對比可知平滑后的點云相較于平滑前的排布更加的緊密規整。
貪婪三角化重構的齒輪測量誤差分析:
采用貪婪三角化算法進行齒輪三維點云重構,其中,圖 7(a)、圖 7(b)為直接利用貪婪投影三角化方法重構的齒輪三維模型,該模型孔洞明顯減少,但模型表面仍然存在諸多噪點,表面粗糙度較高。圖 7(c)、圖 7(d)為平滑后利用貪婪投影三角化算法重構齒輪三維模型,由圖可知平滑后的齒輪表面重構效果更好。

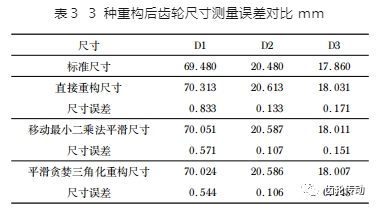
利用直接重構、移動最小二乘法平滑直接重構、平滑加貪婪三角化方法重構 3 種方法得到的齒輪 D1、D2、D3 尺寸測量結果及其測量誤差如表 3 所示,經對比可知,平滑加貪婪三角化方法重構的齒輪尺寸比其他 2 種方法測量誤差小。
四、結論
本文分析了雙目視覺系統提取的齒輪初始三維點云特點,分別采用直通濾波和體素柵格濾波去除了齒輪初始三維點云數據存在的離群點與冗余點;研究了基于移動最小二乘法平滑加貪婪三角化算法的齒輪三維重構方法。搭建了雙目視覺齒輪測量系統實驗平臺,開展直齒圓柱齒輪測量實驗,通過齒輪三維點云數據處理與模型重構,分析了齒輪參數尺寸測量結果及其誤差。實驗結果表明:采用移動最小二乘法平滑加貪婪三角化算法重構后的齒輪三維模型表面平滑,邊緣清晰,其 D1 尺寸測量誤差由 0.833 mm 降至 0.544 mm,D2 由 0.133 mm 降至 0.106 mm,D3 由 0.171 mm 降至 0.148 mm,解決了齒輪三維點云重構模型表面粗糙問題,有效提高了齒輪三維點云的重構精度。
參考文獻略.
