為解決齒輪傳動系統的振動和噪聲問題,研究采用三維拓撲修形方法對面齒輪進行齒廓和齒向修形,并結合集中參數理論和牛頓第二定律構建動力學模型。
通過修形,齒輪傳動系統在各頻段上的噪聲水平顯著降低,總噪聲水平下降了12.0dB。
同時,所構建的動力學模型其振動峰值和振動加速度顯著低于降振前。
研究結果表明,三維拓撲修形方法和動力學模型在降低齒輪傳動系統振動和噪聲方面效果顯著,為齒輪傳動系統的優化設計提供了新的思路,具有重要的工程應用價值。
齒輪傳動系統作為機械設備中的關鍵部件,其性能對整體設備的穩定性和壽命具有重要影響。
然而,振動和噪聲問題是齒輪傳動系統難以避免的問題,其不僅影響設備的正常運行,還可能對周圍環境造成噪音污染。
隨著航空航天、汽車等領域的快速發展,對齒輪傳動系統的減振降噪要求也逐漸提高。
雖然目前針對齒輪傳動系統的減振降噪研究已經取得較好的效果,比如通過改進加工工藝等方法來降低振動和噪聲。
然而,這些方法在實際應用中仍存在效果有限、成本較高等不足。
為了更有效地解決齒輪傳動系統的減振降噪問題,研究采用三維拓撲修形方法對面齒輪進行齒廓和齒向修形,并結合集中參數理論和牛頓第二定律構建動力學模型。
研究期望通過該方法,提高齒輪傳動系統的嚙合性能,降低振動和噪聲,為齒輪傳動系統的減振降噪提供新的思路和方法。
基于此提出了一種新的減振降噪方法,并構建了相應的動力學模型,為齒輪傳動系統的優化設計提供了理論依據。
基于三維拓撲修形的面齒輪減振降噪方法設計:面齒輪傳動因其重合度大和受軸向位移誤差影響小等優勢,被廣泛應用于航空航天和汽車等機械設備領域。
齒輪傳動中振動和噪聲是造成設備性能降低和縮短設備壽命的主要因素之一。
因此尋找一種方法對齒輪傳動系統減振降噪成為當前研究的熱點問題之一。
三維拓撲修形是一種通過對齒輪進行齒廓、齒向的修形,從而降低齒輪噪聲和振動的方法,其具有提高齒輪副的嚙合性能和減少材料浪費等優勢,被廣泛應用于齒輪傳動系統。
因此研究采用三維修行拓撲修形方法對面齒輪副的齒廓和齒向進行修形,齒廓修形和齒向修形方法示意圖如圖1所示。

圖1 齒廓修形和齒向修形方法示意圖
圖1-1為齒廓修形示意圖,圖1-2為采用Litvin等人提出的齒廓修形方法,利用標準齒條刀具對圓柱齒輪的齒廓進行修形的齒條刀具的法向齒廓。
圖中:Oa和Ob為拋物線;ld為Oa和Ob之間的距離;ai為修形系數;Sa和Sb為坐標系;h0為拋物線頂點位置參數;S0為法向齒槽寬;Si為插齒刀和齒條刀具的參數。
其中隨機點在齒條齒廓Sa和Sb的位置可用公式(1)表示。

式中:ra(hi)和rb(hi)分別為齒條齒廓Sa和Sb中的任意一點;Mbara(hi)為Sa至Sb的齊次坐標變換矩陣。齒條刀具齒面在齒條的固聯坐標系中可用公式(2)表示。
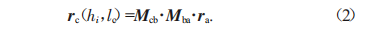
式中:rc(hi,lc)為齒條刀具齒面在齒條的固聯坐標系中的表示;Mcb為Sb到齒條的固聯坐標系的齊次坐標變換矩陣。
在對齒輪加工時利用展成法,利用齒條刀具對齒輪齒面進行加工形成齒面包絡,在這一過程中,齒面上的點從固聯坐標系變換為S1,此時齒輪齒面在S1中可用公式(3)表示。
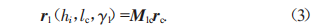
式中:r1(hi,lc,γ1)為S1中齒輪面的公式表示;M1crc為齒條的固聯坐標系到S1的坐標變換矩陣。此外,齒條刀具齒面上的點和齒輪齒面在接觸時需要進行嚙合,其可用公式(4)表示。

由此,面齒輪的齒廓修形完成,接著進行齒向修形。
圖1-3為圓柱齒輪齒向修形的原理圖,其通過工具對齒柱的齒向進行修形。
圖1-4為盤形砂輪齒廓截面圖。圖中:x1,xc為方向;r半徑;z1和zc為坐標系;ac為砂輪和齒廓交點;pc為齒柱和齒柱的距離;y1和y2為方向參數。
在盤形砂輪對圓柱齒輪進行修正時會相互接近,砂輪對圓柱齒輪進行修形時的最短中心距離lc1可用公式(5)表示。

式中:ap為拋物線參數;ld為砂輪與圓柱齒輪在進行修正時相互接近的方向;rp為圓柱齒輪半徑;rc為盤形砂輪半徑。
其中盤形砂輪的曲線、修正后的小圓柱齒輪齒面和解除后的嚙合可用公式(6)表示。

式中:rw為盤形曲線;r1為修形小圓柱齒面;f1為砂輪齒面和圓柱齒面接觸后的嚙合;Nc為法向量;vc為盤形砂輪和小圓柱齒輪的相對速度。
基于減振降噪的面齒輪系統動力學模型設計:在采用齒廓修形和齒向修形方法對面齒輪進行修形以后,研究將集總元件模型理論和加速度定律相結合,建立齒輪系統的動力學模型,該模型如圖2所示。

圖2 基于減振降噪的面齒輪系統動力學模型
圖2中X、Y、Z為面齒輪副繞東方向,在該系統共有14個自由度,其中支承軸為阻尼元件和彈性元件構成,面齒輪、圓柱齒輪、驅動和負載為集中質量。其中,面齒輪系統的自由度{q}可用公式(7)表示。

式中:θE驅動繞軸線的轉動;qg為面齒輪的自由度;θL為負載繞軸線的轉動;qp為圓柱齒輪的自由度。按照牛頓第二定律建立動力學方程,其計算表達式如式(8)所示。
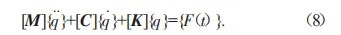
式中:[M]為質量矩陣;[K]為剛度矩陣;[C]為阻尼矩陣;F(t)為外部激勵力。
由于齒輪副的振動反應速度和規模較大,使得計算困難程度增加,從而導致正確解的獲取難以成功。
需要對其進行無量綱處理,進行無量綱處理時需要將時間變量和無量綱時間變量的關系可用公式(9)表示。
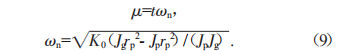
式中:μ為無量綱時間變量;t為時間變量;ωn為無量綱化的嚙合頻率;K0為時變嚙合剛度平均值;rp為主動輪和從動輪的嚙合半徑;Jp和Jg為轉動慣量。
位移變量和無量綱位移變量的關系可用公式(10)表示。

式中:V為位移變量;ζ為無量綱位移變量;bc為位移標稱尺度。由此,根據式(9)和式(10)進行無量綱化處理,得到無量綱化方程,其計算公式如式(11)所示。

式中:c和k分別為無量綱阻尼矩陣和剛度矩陣;f表示載荷矩陣。最后,研究采用Runge-Kutta算法對模型進行求解。
為了對面齒輪的齒廓修形和齒向修形的效果進行分析,研究列出了修形前后齒輪傳動系統的噪聲水平對比,對比結果如表1所示。
從表1中數據可以看出,修形后的噪聲水平在各個頻段上均有顯著降低,總噪聲水平下降了12.0dB。
該結果證明了三維拓撲修形方法在降低齒輪傳動系統振動和噪聲方面的有效性。
此外,為了驗證所構建的系統動力學模型減振性能,進行了修形前后幅值-頻率響應曲線和振動加速度響應實驗測試,其測試結果如圖3所示。
從圖3-1可以看出,研究提出的模型修形后研究提出的模型幅值-響應頻率顯著低于修形前,該結果表明研究提出的模型擁有良好的減振性能。
從圖3-2可知研究提出的模型振動加速度顯著降低。上述結果表明,研究提出的模型擁有良好的減振降噪性能,具有有效性。
綜合以上結果,從降噪和減振維度來看,研究提出的方法和模型具有良好的效果,具有有效性。

圖3 動力學模型修形前后幅值-頻率響應曲線和振動加速度響應曲線
在齒輪傳動系統廣泛應用于機械設備領域的背景下,此次研究旨在解決其振動和噪聲問題。
研究結合三維拓撲修形方法和集中參數理論以及牛頓第二定律等方法,實現了對齒輪傳動系統減振降噪的優化設計。
研究結果顯示,其修形前后分別在50~100Hz、100~200Hz、200~500Hz和500~1000Hz噪聲段降低了10.4dB、9.0dB、13.2dB、12.0dB,且動力學模型振動顯著低于降振前。
該結果表明研究提出的優化設計方法具有良好的減振降噪效果。然而,研究仍存在未考慮不同工況下的修形效果等不足,需在后續研究中進一步完善。
參考文獻:略
第一作者簡介:洪振(1989—),男,遼寧鞍山人,本科,畢業于沈陽航空航天大學,工程師,研究方向為機械設計。
通過修形,齒輪傳動系統在各頻段上的噪聲水平顯著降低,總噪聲水平下降了12.0dB。
同時,所構建的動力學模型其振動峰值和振動加速度顯著低于降振前。
研究結果表明,三維拓撲修形方法和動力學模型在降低齒輪傳動系統振動和噪聲方面效果顯著,為齒輪傳動系統的優化設計提供了新的思路,具有重要的工程應用價值。
引 言
齒輪傳動系統作為機械設備中的關鍵部件,其性能對整體設備的穩定性和壽命具有重要影響。
然而,振動和噪聲問題是齒輪傳動系統難以避免的問題,其不僅影響設備的正常運行,還可能對周圍環境造成噪音污染。
隨著航空航天、汽車等領域的快速發展,對齒輪傳動系統的減振降噪要求也逐漸提高。
雖然目前針對齒輪傳動系統的減振降噪研究已經取得較好的效果,比如通過改進加工工藝等方法來降低振動和噪聲。
然而,這些方法在實際應用中仍存在效果有限、成本較高等不足。
為了更有效地解決齒輪傳動系統的減振降噪問題,研究采用三維拓撲修形方法對面齒輪進行齒廓和齒向修形,并結合集中參數理論和牛頓第二定律構建動力學模型。
研究期望通過該方法,提高齒輪傳動系統的嚙合性能,降低振動和噪聲,為齒輪傳動系統的減振降噪提供新的思路和方法。
基于此提出了一種新的減振降噪方法,并構建了相應的動力學模型,為齒輪傳動系統的優化設計提供了理論依據。
基于減振降噪的齒輪傳動系統研究
基于三維拓撲修形的面齒輪減振降噪方法設計:面齒輪傳動因其重合度大和受軸向位移誤差影響小等優勢,被廣泛應用于航空航天和汽車等機械設備領域。
齒輪傳動中振動和噪聲是造成設備性能降低和縮短設備壽命的主要因素之一。
因此尋找一種方法對齒輪傳動系統減振降噪成為當前研究的熱點問題之一。
三維拓撲修形是一種通過對齒輪進行齒廓、齒向的修形,從而降低齒輪噪聲和振動的方法,其具有提高齒輪副的嚙合性能和減少材料浪費等優勢,被廣泛應用于齒輪傳動系統。
因此研究采用三維修行拓撲修形方法對面齒輪副的齒廓和齒向進行修形,齒廓修形和齒向修形方法示意圖如圖1所示。

圖1 齒廓修形和齒向修形方法示意圖
圖1-1為齒廓修形示意圖,圖1-2為采用Litvin等人提出的齒廓修形方法,利用標準齒條刀具對圓柱齒輪的齒廓進行修形的齒條刀具的法向齒廓。
圖中:Oa和Ob為拋物線;ld為Oa和Ob之間的距離;ai為修形系數;Sa和Sb為坐標系;h0為拋物線頂點位置參數;S0為法向齒槽寬;Si為插齒刀和齒條刀具的參數。
其中隨機點在齒條齒廓Sa和Sb的位置可用公式(1)表示。

式中:ra(hi)和rb(hi)分別為齒條齒廓Sa和Sb中的任意一點;Mbara(hi)為Sa至Sb的齊次坐標變換矩陣。齒條刀具齒面在齒條的固聯坐標系中可用公式(2)表示。
式中:rc(hi,lc)為齒條刀具齒面在齒條的固聯坐標系中的表示;Mcb為Sb到齒條的固聯坐標系的齊次坐標變換矩陣。
在對齒輪加工時利用展成法,利用齒條刀具對齒輪齒面進行加工形成齒面包絡,在這一過程中,齒面上的點從固聯坐標系變換為S1,此時齒輪齒面在S1中可用公式(3)表示。
式中:r1(hi,lc,γ1)為S1中齒輪面的公式表示;M1crc為齒條的固聯坐標系到S1的坐標變換矩陣。此外,齒條刀具齒面上的點和齒輪齒面在接觸時需要進行嚙合,其可用公式(4)表示。
由此,面齒輪的齒廓修形完成,接著進行齒向修形。
圖1-3為圓柱齒輪齒向修形的原理圖,其通過工具對齒柱的齒向進行修形。
圖1-4為盤形砂輪齒廓截面圖。圖中:x1,xc為方向;r半徑;z1和zc為坐標系;ac為砂輪和齒廓交點;pc為齒柱和齒柱的距離;y1和y2為方向參數。
在盤形砂輪對圓柱齒輪進行修正時會相互接近,砂輪對圓柱齒輪進行修形時的最短中心距離lc1可用公式(5)表示。
式中:ap為拋物線參數;ld為砂輪與圓柱齒輪在進行修正時相互接近的方向;rp為圓柱齒輪半徑;rc為盤形砂輪半徑。
其中盤形砂輪的曲線、修正后的小圓柱齒輪齒面和解除后的嚙合可用公式(6)表示。

基于減振降噪的面齒輪系統動力學模型設計:在采用齒廓修形和齒向修形方法對面齒輪進行修形以后,研究將集總元件模型理論和加速度定律相結合,建立齒輪系統的動力學模型,該模型如圖2所示。

圖2 基于減振降噪的面齒輪系統動力學模型
圖2中X、Y、Z為面齒輪副繞東方向,在該系統共有14個自由度,其中支承軸為阻尼元件和彈性元件構成,面齒輪、圓柱齒輪、驅動和負載為集中質量。其中,面齒輪系統的自由度{q}可用公式(7)表示。
式中:θE驅動繞軸線的轉動;qg為面齒輪的自由度;θL為負載繞軸線的轉動;qp為圓柱齒輪的自由度。按照牛頓第二定律建立動力學方程,其計算表達式如式(8)所示。
式中:[M]為質量矩陣;[K]為剛度矩陣;[C]為阻尼矩陣;F(t)為外部激勵力。
由于齒輪副的振動反應速度和規模較大,使得計算困難程度增加,從而導致正確解的獲取難以成功。
需要對其進行無量綱處理,進行無量綱處理時需要將時間變量和無量綱時間變量的關系可用公式(9)表示。
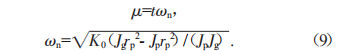
式中:μ為無量綱時間變量;t為時間變量;ωn為無量綱化的嚙合頻率;K0為時變嚙合剛度平均值;rp為主動輪和從動輪的嚙合半徑;Jp和Jg為轉動慣量。
位移變量和無量綱位移變量的關系可用公式(10)表示。
式中:V為位移變量;ζ為無量綱位移變量;bc為位移標稱尺度。由此,根據式(9)和式(10)進行無量綱化處理,得到無量綱化方程,其計算公式如式(11)所示。
式中:c和k分別為無量綱阻尼矩陣和剛度矩陣;f表示載荷矩陣。最后,研究采用Runge-Kutta算法對模型進行求解。
結果分析
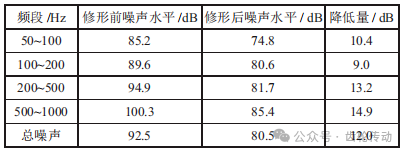
為了對面齒輪的齒廓修形和齒向修形的效果進行分析,研究列出了修形前后齒輪傳動系統的噪聲水平對比,對比結果如表1所示。
從表1中數據可以看出,修形后的噪聲水平在各個頻段上均有顯著降低,總噪聲水平下降了12.0dB。
該結果證明了三維拓撲修形方法在降低齒輪傳動系統振動和噪聲方面的有效性。
表1 修形前后齒輪傳動系統噪聲水平對比

此外,為了驗證所構建的系統動力學模型減振性能,進行了修形前后幅值-頻率響應曲線和振動加速度響應實驗測試,其測試結果如圖3所示。
從圖3-1可以看出,研究提出的模型修形后研究提出的模型幅值-響應頻率顯著低于修形前,該結果表明研究提出的模型擁有良好的減振性能。
從圖3-2可知研究提出的模型振動加速度顯著降低。上述結果表明,研究提出的模型擁有良好的減振降噪性能,具有有效性。
綜合以上結果,從降噪和減振維度來看,研究提出的方法和模型具有良好的效果,具有有效性。

圖3 動力學模型修形前后幅值-頻率響應曲線和振動加速度響應曲線
結 語
在齒輪傳動系統廣泛應用于機械設備領域的背景下,此次研究旨在解決其振動和噪聲問題。
研究結合三維拓撲修形方法和集中參數理論以及牛頓第二定律等方法,實現了對齒輪傳動系統減振降噪的優化設計。
研究結果顯示,其修形前后分別在50~100Hz、100~200Hz、200~500Hz和500~1000Hz噪聲段降低了10.4dB、9.0dB、13.2dB、12.0dB,且動力學模型振動顯著低于降振前。
該結果表明研究提出的優化設計方法具有良好的減振降噪效果。然而,研究仍存在未考慮不同工況下的修形效果等不足,需在后續研究中進一步完善。
參考文獻:略
第一作者簡介:洪振(1989—),男,遼寧鞍山人,本科,畢業于沈陽航空航天大學,工程師,研究方向為機械設計。
