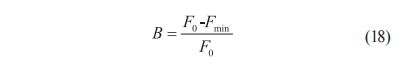編者按:
各位粉絲朋友們,歡迎閱讀本期小編推送的《汽車驅(qū)動(dòng)橋螺旋錐齒輪齒面測(cè)量誤差補(bǔ)償方法》文章。文章主要介紹了提升汽車驅(qū)動(dòng)橋螺旋錐齒輪齒面加工質(zhì)量對(duì)整車的安全與節(jié)能性能有重要意義。
該文針對(duì)汽車驅(qū)動(dòng)橋螺旋錐齒輪實(shí)測(cè)和理論齒面存在的測(cè)量誤差,提出了一種基于對(duì)偶四元數(shù)優(yōu)化的迭代最近點(diǎn)(ICP)齒面測(cè)量誤差補(bǔ)償方法。
本篇文章因篇幅較長(zhǎng),特安排兩期推送。
本期推出:汽車驅(qū)動(dòng)橋螺旋錐齒輪齒面測(cè)量誤差補(bǔ)償方法(一)
提升汽車驅(qū)動(dòng)橋螺旋錐齒輪齒面加工質(zhì)量對(duì)整車的安全與節(jié)能性能有重要意義,該文針對(duì)汽車驅(qū)動(dòng)橋螺旋錐齒輪實(shí)測(cè)和理論齒面存在的測(cè)量誤差,提出了一種基于對(duì)偶四元數(shù)優(yōu)化的迭代最近點(diǎn)(ICP)齒面測(cè)量誤差補(bǔ)償方法。將誤差補(bǔ)償問題轉(zhuǎn)化為兩曲面的配準(zhǔn)問題,利用對(duì)偶四元數(shù)對(duì)齒面配準(zhǔn)模型進(jìn)行表示并得出誤差矩陣,將誤差矩陣線性化并使用凸松弛的全局優(yōu)化算法對(duì)其實(shí)部進(jìn)行優(yōu)化,實(shí)現(xiàn)螺旋錐齒輪齒面的精確配準(zhǔn)。結(jié)果表明:螺旋錐齒輪凹齒面的誤差補(bǔ)償率最高達(dá)77%,最大誤差由補(bǔ)償前的22.11μm降至5.64μm,平均誤差由補(bǔ)償前的10.34μm降至2.38μm,該算法與傳統(tǒng)奇異值分解法(SVD)、四元數(shù)法和Levenberg-Marquardt 法(L-M)相比有更高的求解精度和穩(wěn)定性,證明所提出的補(bǔ)償方法具有可行性。
螺旋錐齒輪是機(jī)械設(shè)備中關(guān)鍵基礎(chǔ)元件之一,廣泛應(yīng)用于汽車、造船、工程機(jī)械、建筑機(jī)械和交通運(yùn)輸機(jī)械等領(lǐng)域。汽車驅(qū)動(dòng)橋螺旋錐齒輪齒面的加工質(zhì)量直接影響主減速器齒輪傳動(dòng)的噪聲、齒輪壽命以及傳遞效率等,進(jìn)而影響到汽車的質(zhì)量和安全性能。精確的齒面測(cè)量和誤差補(bǔ)償可以顯著提高齒輪的嚙合質(zhì)量,減少能量損失,提升傳動(dòng)效率,降低燃油消耗,促進(jìn)汽車節(jié)能。因此,對(duì)驅(qū)動(dòng)橋螺旋錐齒輪齒面測(cè)量誤差進(jìn)行分析和補(bǔ)償具有重要意義。
在齒輪測(cè)量機(jī)測(cè)量汽車驅(qū)動(dòng)橋螺旋錐齒輪齒面的過程中,回轉(zhuǎn)軸傾斜和大端端面加工誤差等多種因素導(dǎo)致理論齒面與實(shí)測(cè)齒面存在偏差。韓連福等分析了齒輪測(cè)量機(jī)的拓?fù)浣Y(jié)構(gòu),由拓?fù)浣Y(jié)果采用多體系統(tǒng)理論建立了齒輪測(cè)量機(jī)幾何誤差補(bǔ)償模型。邢元等提出一種基于歐式線性空間的軟件誤差補(bǔ)償方法,通過 二級(jí)補(bǔ)償機(jī)制有效提高齒面加工精度。宋碧云等基于改進(jìn)的levenberg-marquardt法(levenberg-marquardt,L-M) 并選取敏感性較高的加工參數(shù)對(duì)螺旋錐齒輪齒面誤差進(jìn)行補(bǔ)償。硬件補(bǔ)償方法成本高且零件測(cè)量時(shí)出現(xiàn)的誤差是不可避免的,軟件補(bǔ)償方法是現(xiàn)在的主流方法,但目前存在計(jì)算強(qiáng)度大、迭代不收斂以及誤差補(bǔ)償不夠精確等問題。目前最常用的齒面配準(zhǔn)方法是迭代最近點(diǎn)算法 (iterative closest point,ICP),其實(shí)質(zhì)是基于最小二乘法,將最近點(diǎn)迭代并通過更新兩組曲面數(shù)據(jù)的對(duì)應(yīng)關(guān)系,實(shí)現(xiàn)兩齒面的精確配準(zhǔn)。LIU Yongsheng等用阻尼Gauss-Newton法代ICP算法中奇異值分解法(singular value decomposition,SVD)來求解幾何變換矩陣,有效實(shí)現(xiàn)了測(cè)量齒面向理論齒面的配準(zhǔn)補(bǔ)償,但其容易陷入局部最優(yōu)解。ZHOU Lihua等提出了一種匹配點(diǎn)搜索方法,解決了測(cè)量齒面與理論齒面之間的對(duì)應(yīng)關(guān)系,但其空間復(fù)雜度和時(shí)間復(fù)雜度較高。XIE He等提出了基于點(diǎn)到球面配準(zhǔn)的最近鄰精細(xì)配準(zhǔn)算法,將配準(zhǔn)問題轉(zhuǎn)化為非線性優(yōu)化問題,利用Taylor展開式求解配準(zhǔn)運(yùn)動(dòng)參數(shù),但其需要選擇適當(dāng)?shù)某跏紖?shù)。
為解決現(xiàn)有齒面測(cè)量誤差補(bǔ)償方法存在的問題并實(shí)現(xiàn)理論齒面與實(shí)際齒面偏差的補(bǔ)償,本文首先進(jìn)行兩齒面之間的配準(zhǔn);針對(duì)現(xiàn)有齒面誤差補(bǔ)償方法和ICP算法的局限性,利用對(duì)偶四元數(shù)在同時(shí)處理旋轉(zhuǎn)和平移變換中的優(yōu)勢(shì),提出一種基于對(duì)偶四元數(shù)優(yōu)化的ICP迭代誤差補(bǔ)償算法,以解決傳統(tǒng)ICP方法容易陷入局部最優(yōu)解的問題;利用對(duì)偶四元數(shù)獲取誤差矩陣,將誤差矩陣線性化并進(jìn)行凸松弛優(yōu)化,以此提高齒面配準(zhǔn)的精度和穩(wěn)定性;最后通過實(shí)測(cè)實(shí)驗(yàn)驗(yàn)證本文提出算法的有效性。
1螺旋錐齒輪齒面測(cè)量誤差分析
汽車驅(qū)動(dòng)橋由螺旋錐齒輪、差速器、車輪傳動(dòng)裝置等關(guān)鍵部件組成,作為汽車傳遞動(dòng)力的關(guān)鍵組件,其性能和可靠性直接影響整車的動(dòng)力表現(xiàn)和行駛安全性。 驅(qū)動(dòng)橋螺旋錐齒輪齒面測(cè)量誤差為實(shí)際測(cè)量齒面與理論齒面之間存在的偏差。如圖1所示,在齒輪軸上建立理論坐標(biāo)系 {O: X, Y, Z},螺旋錐齒輪齒面任意 理論測(cè)量點(diǎn)Pi與其對(duì)應(yīng)的實(shí)際測(cè)量點(diǎn)Qi之間的差即為該點(diǎn)齒面偏差δi。當(dāng)測(cè)頭到達(dá)預(yù)設(shè)測(cè)量位置時(shí),實(shí)際測(cè)頭球心C'i與實(shí)測(cè)點(diǎn)Qi都在法向量ni方向上,齒面與測(cè)頭的接觸點(diǎn)Qi處于法線方向nQ上,Qi點(diǎn)到Pi點(diǎn)的距離等于實(shí)際測(cè)頭球心C'i與理論測(cè)頭球心Ci之間的距離di。
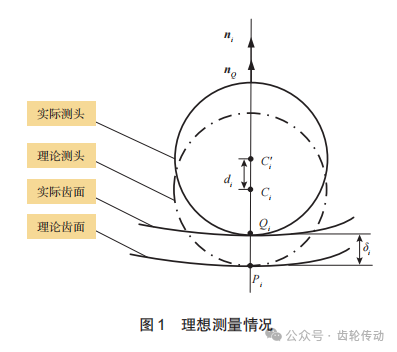 在實(shí)際測(cè)量中,螺旋錐齒輪齒面是連續(xù)光滑曲面,偏心和傾角誤差導(dǎo)致被測(cè)齒面與理論齒面不一致,接觸點(diǎn)處的法線方向與齒面法線方向并不完全一致。如圖2所示,實(shí)際測(cè)頭球心與實(shí)際接觸點(diǎn)Qi不在ni上,接觸點(diǎn)法向nQ與ni也不在同一方向上。理想接觸點(diǎn)Pi與實(shí)際接觸點(diǎn)Qi有一定距離,此時(shí)齒面偏差δi為點(diǎn)Pi到點(diǎn)Qi的距離。
在實(shí)際測(cè)量中,螺旋錐齒輪齒面是連續(xù)光滑曲面,偏心和傾角誤差導(dǎo)致被測(cè)齒面與理論齒面不一致,接觸點(diǎn)處的法線方向與齒面法線方向并不完全一致。如圖2所示,實(shí)際測(cè)頭球心與實(shí)際接觸點(diǎn)Qi不在ni上,接觸點(diǎn)法向nQ與ni也不在同一方向上。理想接觸點(diǎn)Pi與實(shí)際接觸點(diǎn)Qi有一定距離,此時(shí)齒面偏差δi為點(diǎn)Pi到點(diǎn)Qi的距離。
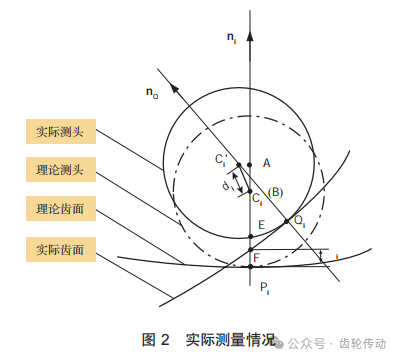 由幾何關(guān)系可知:AB與BE的和為測(cè)頭半徑,由于CNC齒輪測(cè)量機(jī)的測(cè)頭半徑很小,E與Pi的距離非常近,所以PiF的距離近似等于AB的距離,則此時(shí)δi的值可以用式 (1) 近似表示:
由幾何關(guān)系可知:AB與BE的和為測(cè)頭半徑,由于CNC齒輪測(cè)量機(jī)的測(cè)頭半徑很小,E與Pi的距離非常近,所以PiF的距離近似等于AB的距離,則此時(shí)δi的值可以用式 (1) 近似表示:
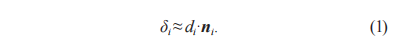 其中:di為實(shí)測(cè)球心與理論球心之間的距離;ni為理論齒面的法向量。
其中:di為實(shí)測(cè)球心與理論球心之間的距離;ni為理論齒面的法向量。
設(shè)理論齒面數(shù)據(jù)點(diǎn)集為P,由{P1, P2, ?Pn} 構(gòu)成,實(shí)際測(cè)量數(shù)據(jù)點(diǎn)集為Q,由{Q1, Q2, ?Qn} 構(gòu)成,齒輪的實(shí)測(cè)齒面測(cè)量點(diǎn)Qi可以由理論齒面數(shù)據(jù)點(diǎn)Pi 、齒面偏差δi和法向量ni表示,如式 (2) 所示:
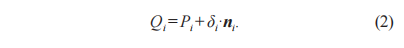 為了減小甚至消除實(shí)測(cè)齒面與理論齒面之間的偏差,需要實(shí)現(xiàn)理論齒面與實(shí)測(cè)齒面的精確配準(zhǔn),利用配準(zhǔn)結(jié)果實(shí)現(xiàn)螺旋錐齒輪的齒面誤差補(bǔ)償。
為了減小甚至消除實(shí)測(cè)齒面與理論齒面之間的偏差,需要實(shí)現(xiàn)理論齒面與實(shí)測(cè)齒面的精確配準(zhǔn),利用配準(zhǔn)結(jié)果實(shí)現(xiàn)螺旋錐齒輪的齒面誤差補(bǔ)償。
2傳統(tǒng)對(duì)偶四元數(shù)算法及齒面配準(zhǔn)模型
對(duì)偶四元數(shù)的形式與性質(zhì):對(duì)偶四元數(shù)表征旋轉(zhuǎn)矩陣和平移向量的方式與傳統(tǒng)方式不同,它們之間存在一定的數(shù)學(xué)關(guān)系。理論點(diǎn)構(gòu)成的坐標(biāo)系O和實(shí)際測(cè)量點(diǎn)構(gòu)成的坐標(biāo)系S之間的變換關(guān)系可以近似地通過一個(gè)平移矢量和一個(gè)單位四元數(shù)來表示,也可以采用一個(gè)更加緊湊和簡(jiǎn)潔的方式來表示,即單位對(duì)偶四元數(shù),如式 (3) 所示:
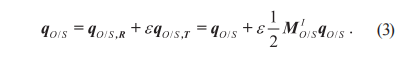 其中:qO/S, R為對(duì)偶四元數(shù)的實(shí)部;qO/S, T為對(duì)偶四元數(shù)的對(duì)偶部;ε是一個(gè)與實(shí)數(shù)域R垂直的維度單位長(zhǎng)度,它滿足ε2=0 ;M1O/S=(0, M1O/S) 代表理論坐標(biāo)系O的原點(diǎn)到實(shí)測(cè)坐標(biāo)系S的原點(diǎn)之間的矢量。式(3)也可以簡(jiǎn)潔表示為式(4):
其中:qO/S, R為對(duì)偶四元數(shù)的實(shí)部;qO/S, T為對(duì)偶四元數(shù)的對(duì)偶部;ε是一個(gè)與實(shí)數(shù)域R垂直的維度單位長(zhǎng)度,它滿足ε2=0 ;M1O/S=(0, M1O/S) 代表理論坐標(biāo)系O的原點(diǎn)到實(shí)測(cè)坐標(biāo)系S的原點(diǎn)之間的矢量。式(3)也可以簡(jiǎn)潔表示為式(4):
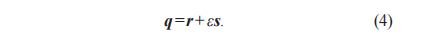 其中:r和s是q的實(shí)部和對(duì)偶部,且r=r1+r2i+r3j+r4k,s= s1+s2i+s3j+s4k ;單位對(duì)偶四元數(shù)滿足單位性和正交性。任意四元數(shù)p和q相乘可以通過矩陣U(p)和W(q)來表示,如式(5) 所示:
其中:r和s是q的實(shí)部和對(duì)偶部,且r=r1+r2i+r3j+r4k,s= s1+s2i+s3j+s4k ;單位對(duì)偶四元數(shù)滿足單位性和正交性。任意四元數(shù)p和q相乘可以通過矩陣U(p)和W(q)來表示,如式(5) 所示:
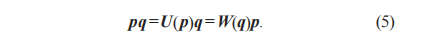 其中,矩陣U(p)和W(q)分別是四元數(shù)p和q的四元數(shù)矩陣,且U(p)稱為W(q)的蛻變矩陣,具體值如式(6)所示:
其中,矩陣U(p)和W(q)分別是四元數(shù)p和q的四元數(shù)矩陣,且U(p)稱為W(q)的蛻變矩陣,具體值如式(6)所示:
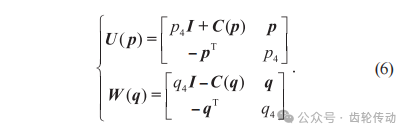 其中:C(p)為偏對(duì)稱矩陣,也稱為反對(duì)稱矩陣,
其中:C(p)為偏對(duì)稱矩陣,也稱為反對(duì)稱矩陣,
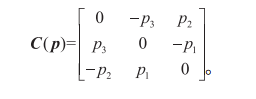 齒面配準(zhǔn)模型:驅(qū)動(dòng)橋螺旋錐齒輪齒面的誤差補(bǔ)償數(shù)學(xué)模型本質(zhì)上是三維空間曲面的相似變換,齒面理論測(cè)量點(diǎn)集P的空間變換用旋轉(zhuǎn)矩陣R和平移矩陣T表示,經(jīng)過空間變換得到點(diǎn)集Q',如式(7)所示:
齒面配準(zhǔn)模型:驅(qū)動(dòng)橋螺旋錐齒輪齒面的誤差補(bǔ)償數(shù)學(xué)模型本質(zhì)上是三維空間曲面的相似變換,齒面理論測(cè)量點(diǎn)集P的空間變換用旋轉(zhuǎn)矩陣R和平移矩陣T表示,經(jīng)過空間變換得到點(diǎn)集Q',如式(7)所示:
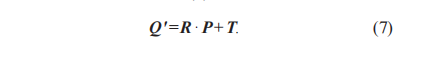 其中,T是由平移向量t構(gòu)成的矩陣。
其中,T是由平移向量t構(gòu)成的矩陣。
點(diǎn)集Q'與實(shí)測(cè)點(diǎn)集Q的差值即為誤差矩陣E,如式(8)所示:
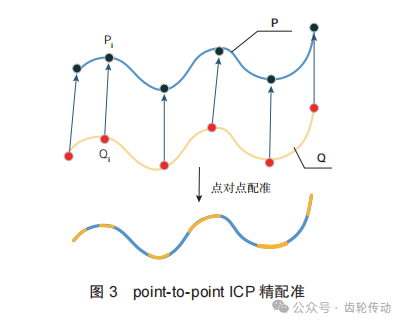
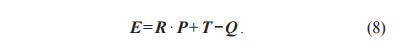 傳統(tǒng)方法選擇距離較大的對(duì)應(yīng)點(diǎn)通過奇異分解 (SVD) 方式獲得變換矩陣R、T。首先根據(jù)參與求解的理論與實(shí)際點(diǎn)云的質(zhì)心構(gòu)造分解矩陣,將其進(jìn)行SVD分解,將矩陣正交對(duì)角化分解得到2個(gè)特征向量矩陣,最后求解得到旋轉(zhuǎn)矩陣R和平移矩陣T。由于螺旋錐齒輪齒面理論點(diǎn)云與測(cè)量點(diǎn)云之間的誤差較小且一一對(duì)應(yīng),不存在噪音點(diǎn),不需要進(jìn)行控制點(diǎn)的選取過程,且不需要對(duì)最近點(diǎn)進(jìn)行搜索,可采用定向點(diǎn)對(duì)點(diǎn)的精配準(zhǔn)方式,如圖3所示。
傳統(tǒng)方法選擇距離較大的對(duì)應(yīng)點(diǎn)通過奇異分解 (SVD) 方式獲得變換矩陣R、T。首先根據(jù)參與求解的理論與實(shí)際點(diǎn)云的質(zhì)心構(gòu)造分解矩陣,將其進(jìn)行SVD分解,將矩陣正交對(duì)角化分解得到2個(gè)特征向量矩陣,最后求解得到旋轉(zhuǎn)矩陣R和平移矩陣T。由于螺旋錐齒輪齒面理論點(diǎn)云與測(cè)量點(diǎn)云之間的誤差較小且一一對(duì)應(yīng),不存在噪音點(diǎn),不需要進(jìn)行控制點(diǎn)的選取過程,且不需要對(duì)最近點(diǎn)進(jìn)行搜索,可采用定向點(diǎn)對(duì)點(diǎn)的精配準(zhǔn)方式,如圖3所示。
 3對(duì)偶四元數(shù)優(yōu)化的ICP迭代算法
3對(duì)偶四元數(shù)優(yōu)化的ICP迭代算法
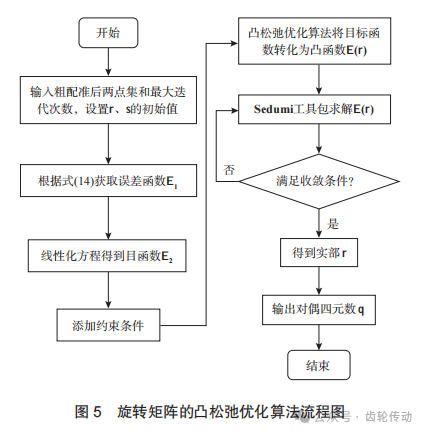
基于對(duì)偶四元數(shù)優(yōu)化的ICP迭代誤差補(bǔ)償算法是以對(duì)偶四元數(shù)的形式將齒面配準(zhǔn)方程分解為旋轉(zhuǎn)矩陣和平移矩陣2部分,獲取誤差矩陣方程并建立新的問題模型,提取同名特征點(diǎn)并將兩點(diǎn)集進(jìn)行粗配準(zhǔn)。為得到更精確的配準(zhǔn)結(jié)果,將誤差矩陣方程線性化并對(duì)其中的旋轉(zhuǎn)矩陣進(jìn)行全局優(yōu)化,使用MATLAB的Sedemi工具進(jìn)行凸松弛優(yōu)化得到全局最優(yōu)解。根據(jù)平均誤差、最大誤差、誤差補(bǔ)償率和方差驗(yàn)證算法補(bǔ)償結(jié)果的準(zhǔn)確性。
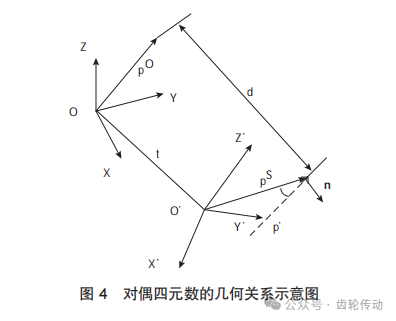
旋轉(zhuǎn)參數(shù)與平移參數(shù)的對(duì)偶四元數(shù)表示:對(duì)偶四元數(shù)的幾何意義可以表示為2個(gè)三維集圍繞著一個(gè)軸做剛體運(yùn)動(dòng),先沿著向量n做平移運(yùn)動(dòng)至p'點(diǎn),平移距離為d,然后在p'點(diǎn)繞向量n旋轉(zhuǎn)θ角度到pS點(diǎn),如圖4所示。
式(4)可以由圖4的幾何關(guān)系重寫,如式(9)所示:
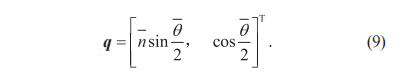
 其中
其中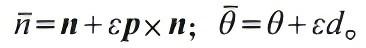 式(4)中的實(shí)部r和對(duì)偶部s與式(9)中n和θ的關(guān)系如式(10)所示:
式(4)中的實(shí)部r和對(duì)偶部s與式(9)中n和θ的關(guān)系如式(10)所示:
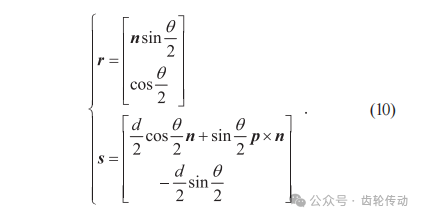 因四元數(shù)法能保持方程是線性的且不產(chǎn)生奇異,任何三維空間的向量都可以用實(shí)部為0的四元數(shù)表示,所以引入2個(gè)以坐標(biāo)向量為正值的純虛四元數(shù),如式(11)所示:
因四元數(shù)法能保持方程是線性的且不產(chǎn)生奇異,任何三維空間的向量都可以用實(shí)部為0的四元數(shù)表示,所以引入2個(gè)以坐標(biāo)向量為正值的純虛四元數(shù),如式(11)所示:
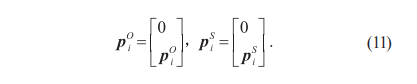 將純四元數(shù)p經(jīng)過四元數(shù)r旋轉(zhuǎn)變換到p',如式(12)所示:
將純四元數(shù)p經(jīng)過四元數(shù)r旋轉(zhuǎn)變換到p',如式(12)所示:
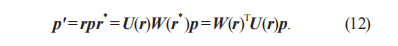 其中,W(r)TU(r)可拓展為矩陣
其中,W(r)TU(r)可拓展為矩陣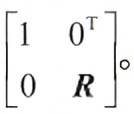 平移四元數(shù)t'的表示如式(13)所示:
平移四元數(shù)t'的表示如式(13)所示:
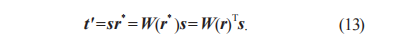 而式(8)可以用對(duì)偶四元數(shù)重新表示,如式(14)所示:
而式(8)可以用對(duì)偶四元數(shù)重新表示,如式(14)所示:
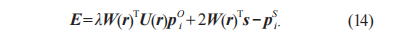 其中:pOi =(xOi , yOi , zOi)T與pSi=(xSi ,ySi ,zSi)T 表示理論測(cè)量點(diǎn)與該點(diǎn)對(duì)應(yīng)的實(shí)際測(cè)量點(diǎn)的控制向量;W(r)TU(r)為旋轉(zhuǎn)矩陣;2W(r)Ts為平移矩陣;λ為比例因子。在螺旋錐齒輪齒面誤差補(bǔ)償算法中,理論齒面和實(shí)測(cè)齒面的整體大小的差別很小,因此本文中涉及的比例因子λ近似為1。
其中:pOi =(xOi , yOi , zOi)T與pSi=(xSi ,ySi ,zSi)T 表示理論測(cè)量點(diǎn)與該點(diǎn)對(duì)應(yīng)的實(shí)際測(cè)量點(diǎn)的控制向量;W(r)TU(r)為旋轉(zhuǎn)矩陣;2W(r)Ts為平移矩陣;λ為比例因子。在螺旋錐齒輪齒面誤差補(bǔ)償算法中,理論齒面和實(shí)測(cè)齒面的整體大小的差別很小,因此本文中涉及的比例因子λ近似為1。
將式(14)進(jìn)行線性化,從實(shí)測(cè)齒面數(shù)據(jù)點(diǎn)與理論齒面數(shù)據(jù)點(diǎn)中提取同名特征點(diǎn),可以得到誤差方程, 如式(15)所示:
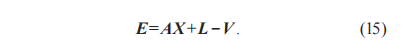 其中:E=(ex, ey, ez)T ,V=(vx, vy, vz)T ,X=(dr1, dr2, dr3, dr4, ds1, ds2, ds3, ds4);A是根據(jù)KD-tree搜索出的點(diǎn)坐標(biāo)構(gòu)成的矩陣;L是與A同名特征點(diǎn)對(duì)應(yīng)的矩陣。
其中:E=(ex, ey, ez)T ,V=(vx, vy, vz)T ,X=(dr1, dr2, dr3, dr4, ds1, ds2, ds3, ds4);A是根據(jù)KD-tree搜索出的點(diǎn)坐標(biāo)構(gòu)成的矩陣;L是與A同名特征點(diǎn)對(duì)應(yīng)的矩陣。
旋轉(zhuǎn)矩陣的全局優(yōu)化:在實(shí)際測(cè)量中,汽車驅(qū)動(dòng)橋螺旋錐齒輪測(cè)量齒面與理論齒面的質(zhì)心相差不大,優(yōu)化兩齒面間的平移向量對(duì)最終誤差補(bǔ)償效果的影響甚微,所以本文僅針對(duì)旋轉(zhuǎn)矩陣進(jìn)行全局優(yōu)化。神經(jīng)網(wǎng)絡(luò)、模擬退火、禁忌搜索等啟發(fā)式全局優(yōu)化算法具有廣泛的適用性,但通常需要調(diào)節(jié)多個(gè)參數(shù)以實(shí)現(xiàn)最佳性能,分支限界法的技巧性更強(qiáng),由于具體問題的差異,分支限界法的具體實(shí)現(xiàn)方法并不具有普適性。凸優(yōu)化方法是通過將目標(biāo)函數(shù)轉(zhuǎn)化為階數(shù)更低的凸函數(shù) ,將可行區(qū)域轉(zhuǎn)化為凸包絡(luò),使多極值非凸優(yōu)化問題轉(zhuǎn)化為凸優(yōu)化問題求解。針對(duì)低階(二次)的非凸函數(shù)優(yōu)化問題,既能保證執(zhí)行效率,又能保證求解的最優(yōu)性。凸松弛優(yōu)化方法最初由D. Hendon等將其應(yīng)用于測(cè)算機(jī)器視覺中的三維重建問題,常用于機(jī)器學(xué)習(xí)、 電力系統(tǒng)等領(lǐng)域,該算法的優(yōu)點(diǎn)是初值不需預(yù)估便獲得最優(yōu)解。為了最大限度確保每次求解的優(yōu)化結(jié)果都能收斂到全局最優(yōu)解,本文提出將對(duì)偶四元數(shù)與凸松弛優(yōu)化算法結(jié)合進(jìn)行求解。為了避免求解過程中出現(xiàn)2個(gè)最優(yōu)解的情況,同時(shí)確保特征點(diǎn)求解的數(shù)值穩(wěn)定性,增加約束條件 r·sT=0和rT·r=1,并在確定松弛系數(shù)后,利用線性矩陣建立凸優(yōu)化模型。以最小化方程式(8)為幾何誤差目標(biāo)函數(shù),以對(duì)偶四元數(shù)的性質(zhì)為約束條件,建立二階多項(xiàng)式優(yōu)化問題并進(jìn)行優(yōu)化,具體步驟如下。
步驟1:確定最大迭代次數(shù),定義對(duì)偶四元數(shù)變量:r=(r1, r2, r3, r4)T ,s=(s1, s2, s3, s4)T,初始值 r=(1, 0, 0, 0)T,s=(0, 0, 0, 0)T,建立目標(biāo)函數(shù)minf(r),如式 (16) 所示:
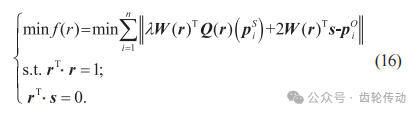 步驟2:確定松弛系數(shù),將線性化后的式(15)引入,確定凸優(yōu)化模型,如式(17)所示:
步驟2:確定松弛系數(shù),將線性化后的式(15)引入,確定凸優(yōu)化模型,如式(17)所示:
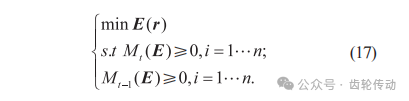 其中,當(dāng)Mt(E)與Mt-1(E)滿秩時(shí),才能得到全局優(yōu)化解,進(jìn)行下一步。
其中,當(dāng)Mt(E)與Mt-1(E)滿秩時(shí),才能得到全局優(yōu)化解,進(jìn)行下一步。
步驟3:通過調(diào)用線性優(yōu)化求解器Sedumi工具箱得到最優(yōu)解,進(jìn)而得到對(duì)偶數(shù)實(shí)部r。
步驟4:將得到的r代入式(17)中得到對(duì)偶部s。
步驟5:輸出對(duì)偶四元數(shù)q。
旋轉(zhuǎn)矩陣的凸松弛優(yōu)化流程如圖5所示。
 對(duì)偶四元數(shù)轉(zhuǎn)換坐標(biāo)的精度計(jì)算:
對(duì)偶四元數(shù)轉(zhuǎn)換坐標(biāo)的精度計(jì)算:
確定參數(shù)精度的必要性在于確保對(duì)偶四元數(shù)模型的可靠性和準(zhǔn)確性,便于有效地描述和預(yù)測(cè)復(fù)雜算法的行為。基于對(duì)偶四元數(shù)優(yōu)化的ICP迭代算法獲得的最終結(jié)果,需要通過計(jì)算精確度來驗(yàn)證算法的有效性。設(shè)理論點(diǎn)集P和測(cè)量點(diǎn)集Q對(duì)應(yīng)各點(diǎn)的歐式距離為fi',由此得出對(duì)應(yīng)點(diǎn)的歐式距離和F0=Σfi',將基于對(duì)偶四元數(shù)優(yōu)化的配準(zhǔn)算法與現(xiàn)有文獻(xiàn)提出的其他配準(zhǔn)算法的結(jié)果進(jìn)行對(duì)比。本文將算法配準(zhǔn)后最小歐氏距離和Fmin設(shè)定為最終誤差。在此基礎(chǔ)上定義B為整體誤差補(bǔ)償率來驗(yàn)證算法的精確度,如式(18)所示:
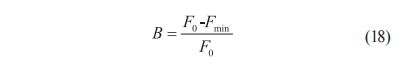 進(jìn)一步定量分析配準(zhǔn)的精度,引入平均誤差
進(jìn)一步定量分析配準(zhǔn)的精度,引入平均誤差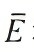 和方差s2E,
和方差s2E,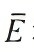 是指補(bǔ)償后齒面對(duì)應(yīng)點(diǎn)之間距離的均值,可以評(píng)判補(bǔ)償算法的優(yōu)劣性,s2E 是對(duì)應(yīng)點(diǎn)之間距離與均值之差的平方和的平均值,可以反映各點(diǎn)補(bǔ)償結(jié)果的離散程度。
是指補(bǔ)償后齒面對(duì)應(yīng)點(diǎn)之間距離的均值,可以評(píng)判補(bǔ)償算法的優(yōu)劣性,s2E 是對(duì)應(yīng)點(diǎn)之間距離與均值之差的平方和的平均值,可以反映各點(diǎn)補(bǔ)償結(jié)果的離散程度。
各位粉絲朋友們,歡迎閱讀本期小編推送的《汽車驅(qū)動(dòng)橋螺旋錐齒輪齒面測(cè)量誤差補(bǔ)償方法》文章。文章主要介紹了提升汽車驅(qū)動(dòng)橋螺旋錐齒輪齒面加工質(zhì)量對(duì)整車的安全與節(jié)能性能有重要意義。
該文針對(duì)汽車驅(qū)動(dòng)橋螺旋錐齒輪實(shí)測(cè)和理論齒面存在的測(cè)量誤差,提出了一種基于對(duì)偶四元數(shù)優(yōu)化的迭代最近點(diǎn)(ICP)齒面測(cè)量誤差補(bǔ)償方法。
本篇文章因篇幅較長(zhǎng),特安排兩期推送。
本期推出:汽車驅(qū)動(dòng)橋螺旋錐齒輪齒面測(cè)量誤差補(bǔ)償方法(一)
提升汽車驅(qū)動(dòng)橋螺旋錐齒輪齒面加工質(zhì)量對(duì)整車的安全與節(jié)能性能有重要意義,該文針對(duì)汽車驅(qū)動(dòng)橋螺旋錐齒輪實(shí)測(cè)和理論齒面存在的測(cè)量誤差,提出了一種基于對(duì)偶四元數(shù)優(yōu)化的迭代最近點(diǎn)(ICP)齒面測(cè)量誤差補(bǔ)償方法。將誤差補(bǔ)償問題轉(zhuǎn)化為兩曲面的配準(zhǔn)問題,利用對(duì)偶四元數(shù)對(duì)齒面配準(zhǔn)模型進(jìn)行表示并得出誤差矩陣,將誤差矩陣線性化并使用凸松弛的全局優(yōu)化算法對(duì)其實(shí)部進(jìn)行優(yōu)化,實(shí)現(xiàn)螺旋錐齒輪齒面的精確配準(zhǔn)。結(jié)果表明:螺旋錐齒輪凹齒面的誤差補(bǔ)償率最高達(dá)77%,最大誤差由補(bǔ)償前的22.11μm降至5.64μm,平均誤差由補(bǔ)償前的10.34μm降至2.38μm,該算法與傳統(tǒng)奇異值分解法(SVD)、四元數(shù)法和Levenberg-Marquardt 法(L-M)相比有更高的求解精度和穩(wěn)定性,證明所提出的補(bǔ)償方法具有可行性。
螺旋錐齒輪是機(jī)械設(shè)備中關(guān)鍵基礎(chǔ)元件之一,廣泛應(yīng)用于汽車、造船、工程機(jī)械、建筑機(jī)械和交通運(yùn)輸機(jī)械等領(lǐng)域。汽車驅(qū)動(dòng)橋螺旋錐齒輪齒面的加工質(zhì)量直接影響主減速器齒輪傳動(dòng)的噪聲、齒輪壽命以及傳遞效率等,進(jìn)而影響到汽車的質(zhì)量和安全性能。精確的齒面測(cè)量和誤差補(bǔ)償可以顯著提高齒輪的嚙合質(zhì)量,減少能量損失,提升傳動(dòng)效率,降低燃油消耗,促進(jìn)汽車節(jié)能。因此,對(duì)驅(qū)動(dòng)橋螺旋錐齒輪齒面測(cè)量誤差進(jìn)行分析和補(bǔ)償具有重要意義。
在齒輪測(cè)量機(jī)測(cè)量汽車驅(qū)動(dòng)橋螺旋錐齒輪齒面的過程中,回轉(zhuǎn)軸傾斜和大端端面加工誤差等多種因素導(dǎo)致理論齒面與實(shí)測(cè)齒面存在偏差。韓連福等分析了齒輪測(cè)量機(jī)的拓?fù)浣Y(jié)構(gòu),由拓?fù)浣Y(jié)果采用多體系統(tǒng)理論建立了齒輪測(cè)量機(jī)幾何誤差補(bǔ)償模型。邢元等提出一種基于歐式線性空間的軟件誤差補(bǔ)償方法,通過 二級(jí)補(bǔ)償機(jī)制有效提高齒面加工精度。宋碧云等基于改進(jìn)的levenberg-marquardt法(levenberg-marquardt,L-M) 并選取敏感性較高的加工參數(shù)對(duì)螺旋錐齒輪齒面誤差進(jìn)行補(bǔ)償。硬件補(bǔ)償方法成本高且零件測(cè)量時(shí)出現(xiàn)的誤差是不可避免的,軟件補(bǔ)償方法是現(xiàn)在的主流方法,但目前存在計(jì)算強(qiáng)度大、迭代不收斂以及誤差補(bǔ)償不夠精確等問題。目前最常用的齒面配準(zhǔn)方法是迭代最近點(diǎn)算法 (iterative closest point,ICP),其實(shí)質(zhì)是基于最小二乘法,將最近點(diǎn)迭代并通過更新兩組曲面數(shù)據(jù)的對(duì)應(yīng)關(guān)系,實(shí)現(xiàn)兩齒面的精確配準(zhǔn)。LIU Yongsheng等用阻尼Gauss-Newton法代ICP算法中奇異值分解法(singular value decomposition,SVD)來求解幾何變換矩陣,有效實(shí)現(xiàn)了測(cè)量齒面向理論齒面的配準(zhǔn)補(bǔ)償,但其容易陷入局部最優(yōu)解。ZHOU Lihua等提出了一種匹配點(diǎn)搜索方法,解決了測(cè)量齒面與理論齒面之間的對(duì)應(yīng)關(guān)系,但其空間復(fù)雜度和時(shí)間復(fù)雜度較高。XIE He等提出了基于點(diǎn)到球面配準(zhǔn)的最近鄰精細(xì)配準(zhǔn)算法,將配準(zhǔn)問題轉(zhuǎn)化為非線性優(yōu)化問題,利用Taylor展開式求解配準(zhǔn)運(yùn)動(dòng)參數(shù),但其需要選擇適當(dāng)?shù)某跏紖?shù)。
為解決現(xiàn)有齒面測(cè)量誤差補(bǔ)償方法存在的問題并實(shí)現(xiàn)理論齒面與實(shí)際齒面偏差的補(bǔ)償,本文首先進(jìn)行兩齒面之間的配準(zhǔn);針對(duì)現(xiàn)有齒面誤差補(bǔ)償方法和ICP算法的局限性,利用對(duì)偶四元數(shù)在同時(shí)處理旋轉(zhuǎn)和平移變換中的優(yōu)勢(shì),提出一種基于對(duì)偶四元數(shù)優(yōu)化的ICP迭代誤差補(bǔ)償算法,以解決傳統(tǒng)ICP方法容易陷入局部最優(yōu)解的問題;利用對(duì)偶四元數(shù)獲取誤差矩陣,將誤差矩陣線性化并進(jìn)行凸松弛優(yōu)化,以此提高齒面配準(zhǔn)的精度和穩(wěn)定性;最后通過實(shí)測(cè)實(shí)驗(yàn)驗(yàn)證本文提出算法的有效性。
1螺旋錐齒輪齒面測(cè)量誤差分析
汽車驅(qū)動(dòng)橋由螺旋錐齒輪、差速器、車輪傳動(dòng)裝置等關(guān)鍵部件組成,作為汽車傳遞動(dòng)力的關(guān)鍵組件,其性能和可靠性直接影響整車的動(dòng)力表現(xiàn)和行駛安全性。 驅(qū)動(dòng)橋螺旋錐齒輪齒面測(cè)量誤差為實(shí)際測(cè)量齒面與理論齒面之間存在的偏差。如圖1所示,在齒輪軸上建立理論坐標(biāo)系 {O: X, Y, Z},螺旋錐齒輪齒面任意 理論測(cè)量點(diǎn)Pi與其對(duì)應(yīng)的實(shí)際測(cè)量點(diǎn)Qi之間的差即為該點(diǎn)齒面偏差δi。當(dāng)測(cè)頭到達(dá)預(yù)設(shè)測(cè)量位置時(shí),實(shí)際測(cè)頭球心C'i與實(shí)測(cè)點(diǎn)Qi都在法向量ni方向上,齒面與測(cè)頭的接觸點(diǎn)Qi處于法線方向nQ上,Qi點(diǎn)到Pi點(diǎn)的距離等于實(shí)際測(cè)頭球心C'i與理論測(cè)頭球心Ci之間的距離di。


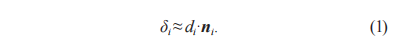
設(shè)理論齒面數(shù)據(jù)點(diǎn)集為P,由{P1, P2, ?Pn} 構(gòu)成,實(shí)際測(cè)量數(shù)據(jù)點(diǎn)集為Q,由{Q1, Q2, ?Qn} 構(gòu)成,齒輪的實(shí)測(cè)齒面測(cè)量點(diǎn)Qi可以由理論齒面數(shù)據(jù)點(diǎn)Pi 、齒面偏差δi和法向量ni表示,如式 (2) 所示:
2傳統(tǒng)對(duì)偶四元數(shù)算法及齒面配準(zhǔn)模型
對(duì)偶四元數(shù)的形式與性質(zhì):對(duì)偶四元數(shù)表征旋轉(zhuǎn)矩陣和平移向量的方式與傳統(tǒng)方式不同,它們之間存在一定的數(shù)學(xué)關(guān)系。理論點(diǎn)構(gòu)成的坐標(biāo)系O和實(shí)際測(cè)量點(diǎn)構(gòu)成的坐標(biāo)系S之間的變換關(guān)系可以近似地通過一個(gè)平移矢量和一個(gè)單位四元數(shù)來表示,也可以采用一個(gè)更加緊湊和簡(jiǎn)潔的方式來表示,即單位對(duì)偶四元數(shù),如式 (3) 所示:
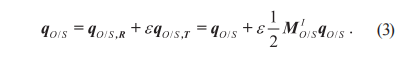
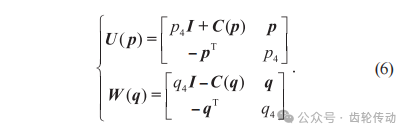
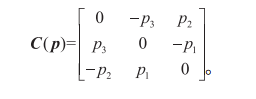
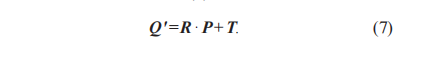
點(diǎn)集Q'與實(shí)測(cè)點(diǎn)集Q的差值即為誤差矩陣E,如式(8)所示:
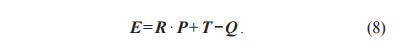

基于對(duì)偶四元數(shù)優(yōu)化的ICP迭代誤差補(bǔ)償算法是以對(duì)偶四元數(shù)的形式將齒面配準(zhǔn)方程分解為旋轉(zhuǎn)矩陣和平移矩陣2部分,獲取誤差矩陣方程并建立新的問題模型,提取同名特征點(diǎn)并將兩點(diǎn)集進(jìn)行粗配準(zhǔn)。為得到更精確的配準(zhǔn)結(jié)果,將誤差矩陣方程線性化并對(duì)其中的旋轉(zhuǎn)矩陣進(jìn)行全局優(yōu)化,使用MATLAB的Sedemi工具進(jìn)行凸松弛優(yōu)化得到全局最優(yōu)解。根據(jù)平均誤差、最大誤差、誤差補(bǔ)償率和方差驗(yàn)證算法補(bǔ)償結(jié)果的準(zhǔn)確性。
旋轉(zhuǎn)參數(shù)與平移參數(shù)的對(duì)偶四元數(shù)表示:對(duì)偶四元數(shù)的幾何意義可以表示為2個(gè)三維集圍繞著一個(gè)軸做剛體運(yùn)動(dòng),先沿著向量n做平移運(yùn)動(dòng)至p'點(diǎn),平移距離為d,然后在p'點(diǎn)繞向量n旋轉(zhuǎn)θ角度到pS點(diǎn),如圖4所示。
式(4)可以由圖4的幾何關(guān)系重寫,如式(9)所示:
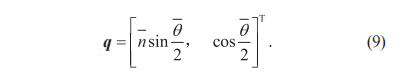

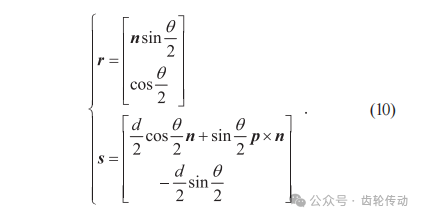
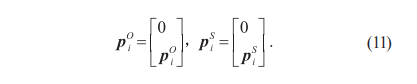
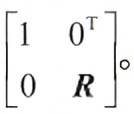 平移四元數(shù)t'的表示如式(13)所示:
平移四元數(shù)t'的表示如式(13)所示:將式(14)進(jìn)行線性化,從實(shí)測(cè)齒面數(shù)據(jù)點(diǎn)與理論齒面數(shù)據(jù)點(diǎn)中提取同名特征點(diǎn),可以得到誤差方程, 如式(15)所示:
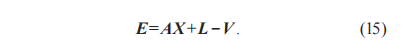
旋轉(zhuǎn)矩陣的全局優(yōu)化:在實(shí)際測(cè)量中,汽車驅(qū)動(dòng)橋螺旋錐齒輪測(cè)量齒面與理論齒面的質(zhì)心相差不大,優(yōu)化兩齒面間的平移向量對(duì)最終誤差補(bǔ)償效果的影響甚微,所以本文僅針對(duì)旋轉(zhuǎn)矩陣進(jìn)行全局優(yōu)化。神經(jīng)網(wǎng)絡(luò)、模擬退火、禁忌搜索等啟發(fā)式全局優(yōu)化算法具有廣泛的適用性,但通常需要調(diào)節(jié)多個(gè)參數(shù)以實(shí)現(xiàn)最佳性能,分支限界法的技巧性更強(qiáng),由于具體問題的差異,分支限界法的具體實(shí)現(xiàn)方法并不具有普適性。凸優(yōu)化方法是通過將目標(biāo)函數(shù)轉(zhuǎn)化為階數(shù)更低的凸函數(shù) ,將可行區(qū)域轉(zhuǎn)化為凸包絡(luò),使多極值非凸優(yōu)化問題轉(zhuǎn)化為凸優(yōu)化問題求解。針對(duì)低階(二次)的非凸函數(shù)優(yōu)化問題,既能保證執(zhí)行效率,又能保證求解的最優(yōu)性。凸松弛優(yōu)化方法最初由D. Hendon等將其應(yīng)用于測(cè)算機(jī)器視覺中的三維重建問題,常用于機(jī)器學(xué)習(xí)、 電力系統(tǒng)等領(lǐng)域,該算法的優(yōu)點(diǎn)是初值不需預(yù)估便獲得最優(yōu)解。為了最大限度確保每次求解的優(yōu)化結(jié)果都能收斂到全局最優(yōu)解,本文提出將對(duì)偶四元數(shù)與凸松弛優(yōu)化算法結(jié)合進(jìn)行求解。為了避免求解過程中出現(xiàn)2個(gè)最優(yōu)解的情況,同時(shí)確保特征點(diǎn)求解的數(shù)值穩(wěn)定性,增加約束條件 r·sT=0和rT·r=1,并在確定松弛系數(shù)后,利用線性矩陣建立凸優(yōu)化模型。以最小化方程式(8)為幾何誤差目標(biāo)函數(shù),以對(duì)偶四元數(shù)的性質(zhì)為約束條件,建立二階多項(xiàng)式優(yōu)化問題并進(jìn)行優(yōu)化,具體步驟如下。
步驟1:確定最大迭代次數(shù),定義對(duì)偶四元數(shù)變量:r=(r1, r2, r3, r4)T ,s=(s1, s2, s3, s4)T,初始值 r=(1, 0, 0, 0)T,s=(0, 0, 0, 0)T,建立目標(biāo)函數(shù)minf(r),如式 (16) 所示:
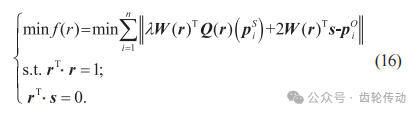
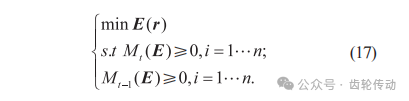
步驟3:通過調(diào)用線性優(yōu)化求解器Sedumi工具箱得到最優(yōu)解,進(jìn)而得到對(duì)偶數(shù)實(shí)部r。
步驟4:將得到的r代入式(17)中得到對(duì)偶部s。
步驟5:輸出對(duì)偶四元數(shù)q。
旋轉(zhuǎn)矩陣的凸松弛優(yōu)化流程如圖5所示。

確定參數(shù)精度的必要性在于確保對(duì)偶四元數(shù)模型的可靠性和準(zhǔn)確性,便于有效地描述和預(yù)測(cè)復(fù)雜算法的行為。基于對(duì)偶四元數(shù)優(yōu)化的ICP迭代算法獲得的最終結(jié)果,需要通過計(jì)算精確度來驗(yàn)證算法的有效性。設(shè)理論點(diǎn)集P和測(cè)量點(diǎn)集Q對(duì)應(yīng)各點(diǎn)的歐式距離為fi',由此得出對(duì)應(yīng)點(diǎn)的歐式距離和F0=Σfi',將基于對(duì)偶四元數(shù)優(yōu)化的配準(zhǔn)算法與現(xiàn)有文獻(xiàn)提出的其他配準(zhǔn)算法的結(jié)果進(jìn)行對(duì)比。本文將算法配準(zhǔn)后最小歐氏距離和Fmin設(shè)定為最終誤差。在此基礎(chǔ)上定義B為整體誤差補(bǔ)償率來驗(yàn)證算法的精確度,如式(18)所示: